Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- 진법변환 #2to10 #10to2 #이진법 #십진법 #변환 #bitset #c++
- 22869
- 호반우 상인
- 16202
- c++ #boj #
- 3D #Reconstruction #computer #vision #volume #metric #tsdf #kinect #fusion
- N번째큰수
- boj #백준
- hcpc
- graph
- BOJ
- 20117
- 이분탐색 #dp #11053
- 최소 #공배수 #최대 #공약수 #유클리드 #호제법 #lcm #gcd #c++ #boj #3343 #백준 #장미
- LIS #가장긴증가하는부분수열 #
- c++ #입출력 #속도 #ios #sync_with_stdio #cin #cout #tie
- 코딩
- 쌤쌤쌤
- 3343
- graph #최단경로
- C++
- 30870
- backtracking #codetree #디버깅 #삼성코테
- 레드아보
- 백준 #다익스트라 #dijkstra #9370 #c++
- 백준
- 1174
- 줄어드는수
- 사이클 없는 그래프
- 투포인터 #백준 #boj #20922 #22862
Archives
- Today
- Total
hyunjin
[가장 긴 증가하는 부분 수열] LIS, DP, 이분탐색 본문
728x90
https://www.acmicpc.net/problem/11053
11053번: 가장 긴 증가하는 부분 수열
수열 A가 주어졌을 때, 가장 긴 증가하는 부분 수열을 구하는 프로그램을 작성하시오. 예를 들어, 수열 A = {10, 20, 10, 30, 20, 50} 인 경우에 가장 긴 증가하는 부분 수열은 A = {10, 20, 10, 30, 20, 50} 이
www.acmicpc.net
최장 증가 수열 (LIS, Longest Increasing Subsequence)
다이나믹 프로그래밍을 이용한 방법 : O(N^2)
- 최장 길이 구하는 방법
앞 순서의 모든 원소에서 끝나는 최장 증가 수열들의 길이 중 가장 긴 것을 골라 1을 더한 것이 곧 현재 수에서 끝나는 최장 증가 수열의 길이이다.
따라서 dp[i] = "i번째 인덱스에서 끝나는 최장 증가 수열의 길이"로 정의한다.
void LIS_DP() {
for (int i = 0; i < N; i++) {
dp[i] = 1;
for (int j = 0; j < i; j++) {
if (arr[j] < arr[i])
dp[i] = max(dp[i], dp[j] + 1);
}
}
}
이분 탐색을 이용한 방법 : O(NlogN)
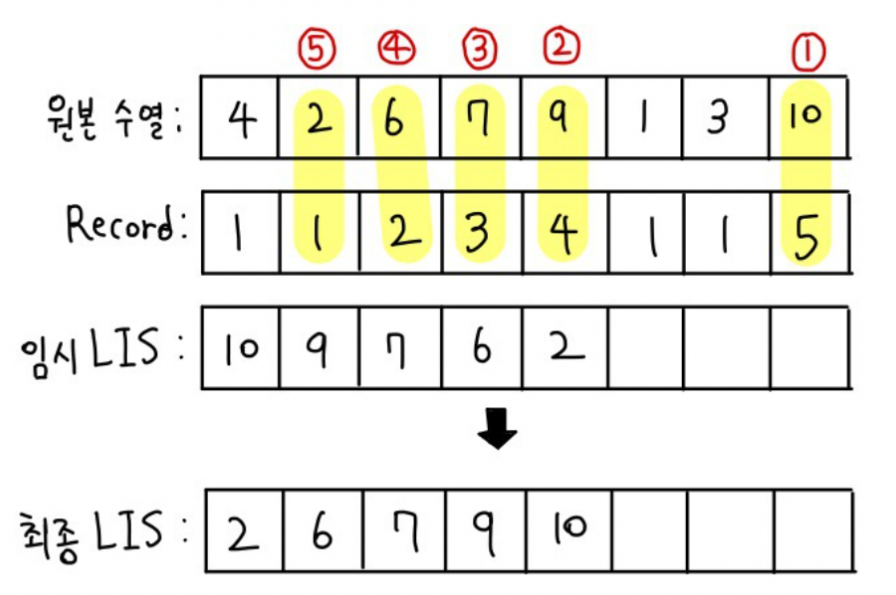
rec 보고 최종 LIS 구할 수 있음
rec에서 N-1부터 찾아가면 LIS 배열 찾을 수 있음.
int Rec[N];
vector<int> LIS;
int BS(int left,int right,int val) {
while (left < right) {
int mid = (left + right) / 2;
if (LIS[mid] < val) left = mid + 1;
else right = mid;
}
return right;
}
int LIS_BS() {
int ret = 1; // LIS 길이
LIS.push_back(arr[0]);
Rec[0] = 0; //LIS에서 순서
for (int i = 1; i < N; i++) {
if (LIS.back() < arr[i]) {
LIS.push_back(arr[i]);
ret++;
}
int pos = BS(0, LIS.size() - 1, arr[i]);
Rec[i] = pos;
LIS[pos] = arr[i];
}
return ret+1;
}
728x90
'알고리즘 연습 > 백준' 카테고리의 다른 글
| [BOJ 9370 미확인 도착지] 다익스트라 dijkstra 그래프 최단경로 (0) | 2024.04.22 |
|---|---|
| [투포인터 BOJ20922 BOJ22862] (0) | 2024.04.20 |
| [BOJ 15663/15664 c++]N과 M, set, backtracking (0) | 2022.10.01 |
| [C++][BOJ 7662 이중 우선순위 큐] multiset (0) | 2021.12.15 |
| [C++][BOJ 1629 곱셈] pow 연산 줄이기 (0) | 2021.12.06 |


