| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 3D #Reconstruction #computer #vision #volume #metric #tsdf #kinect #fusion
- C++
- N번째큰수
- 진법변환 #2to10 #10to2 #이진법 #십진법 #변환 #bitset #c++
- graph
- 사이클 없는 그래프
- 1174
- 코딩
- backtracking #codetree #디버깅 #삼성코테
- BOJ
- graph #최단경로
- 백준
- 30870
- 최소 #공배수 #최대 #공약수 #유클리드 #호제법 #lcm #gcd #c++ #boj #3343 #백준 #장미
- hcpc
- 16202
- 레드아보
- 이분탐색 #dp #11053
- c++ #boj #
- 호반우 상인
- 쌤쌤쌤
- LIS #가장긴증가하는부분수열 #
- c++ #입출력 #속도 #ios #sync_with_stdio #cin #cout #tie
- boj #백준
- 줄어드는수
- 백준 #다익스트라 #dijkstra #9370 #c++
- 투포인터 #백준 #boj #20922 #22862
- 3343
- 20117
- 22869
- Today
- Total
hyunjin
좌표계, 좌표계 변환 본문
영상 geometry에 크게 4가지 좌표계 존재

1. 월드 좌표계 (World Coordinate System)
- 우리가 살고 있는 공간의 한 지점을 기준으로한 좌표계
- - 사물,물체 위치를 표현할 때 기준으로 삼는 좌표계
- - 문제에 따라 임의로 잡아 사용할 수 있는 좌표계, 축도
- - 좌표의 잔위는 meter,centimeter 뭘로 해도 되나 어떤 점이 어떤 위치인지 그 문제 내에서 만큼 유일하게 결정될 수 있어야 함.
$ P = (X,Y,Z) $
월드 좌표계가 우리가 살고 있는 공간의 한 지점이라면 카메라 좌표계는 카메라를 기준으로 함
2. 카메라 좌표계
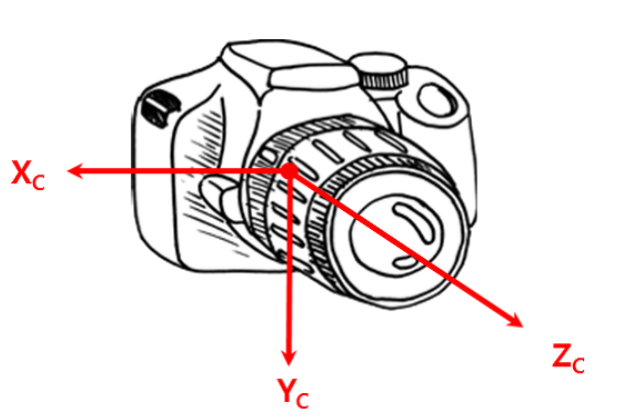
- - 카메라 정면 광학축 방향 Z축
- - 카메라 아래 방향 Y
- - 오른쪽 X
- - 카메라 좌표계의 단위는 월드 좌표계와 동일해야 함, 월드가 m 쓰면 여기도 m 단위
$ P = (X_c,Y_c,Z_c) $
3. 픽셀 좌표계, 영상 좌표계 (Pixel Image Coordinate System)
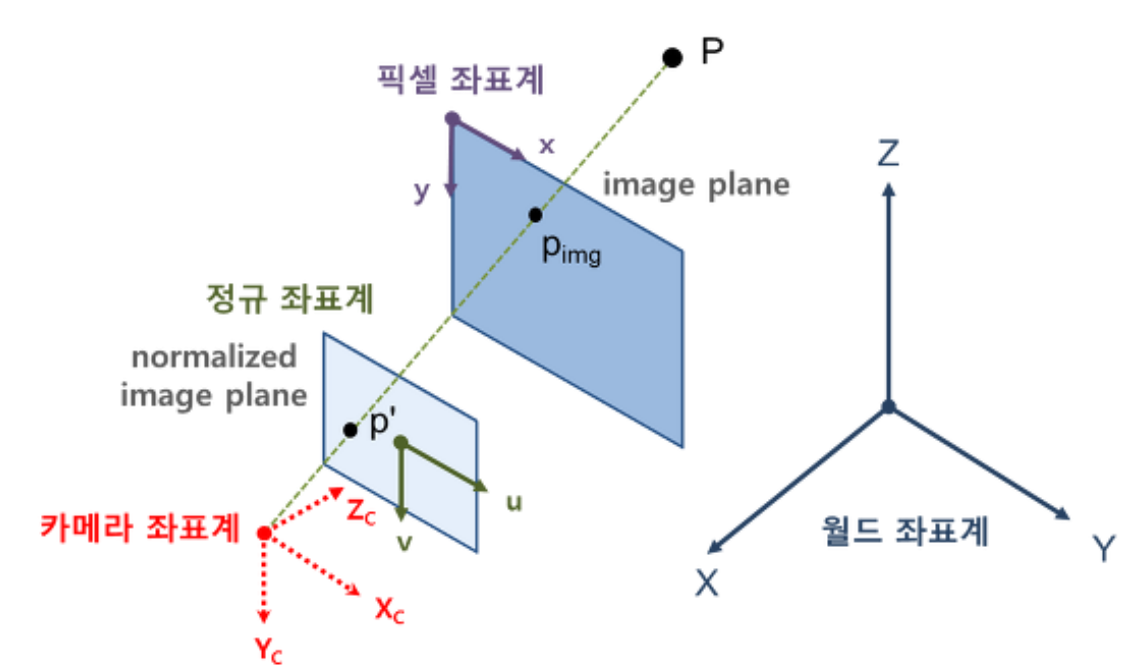
- 우리가 실제 눈으로 보는 영상에 대한 좌표계, 이미지 왼쪽 상단 모서리 원점
- 픽셀 좌표계의 x축, y축에 의해 결정되는 평면을 이미지 평면 (image plane)
- 단위는 pixel
기하학적으로 볼 때, 3D 공간상의 한 점 P = (X,Y,Z)는
카메라의 초점 (또는 렌즈의 초점)을 지나서 이미지 평면의 한 점 $p_{img}$에 투영(projection)
점 P와 점 $p_{img}$를 잊는 선(ray) 상에 있는 모든 3D 점들은 모두 pimg로 투영됩니다.
따라서 3D 점 P로부터 $p_{img}$는 유일하게 결정할 수 있지만, 반대로 영상 픽셀 $p_{img}$로부터 P를 구하는 것은 부가적인 정보 없이는 불가능합니다.
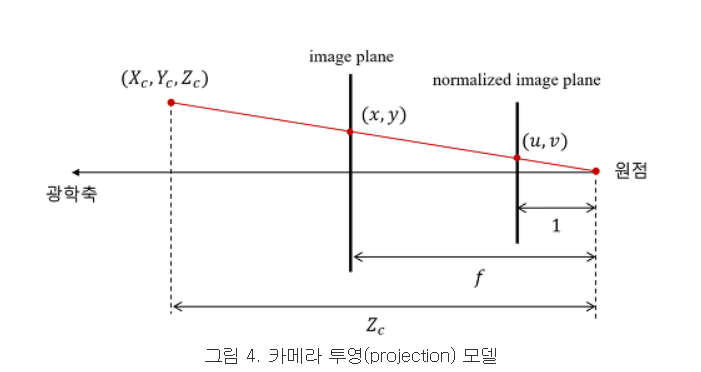
4. 정규 좌표계(Normalized Image Coordinate System)
- - 카메라의 내부 파라미터(intrinsic parameter)의 영향을 제거한 이미지 좌표계
- 좌표계의 단위를 없앤(정규화된) 좌표계이며 카메라 초점과의 거리가 1인 가상의 이미지 평면을 정의하는 좌표계
- →원래의 이미지 평면을 평행이동시켜서 카메라 초점과의 거리가 1인 지점으로 옮겨놓은 이미지 평면
- - 원점은 정규 이미지 평면의 중점(광학축 Zc와의 교점)
${p'} = (u ,v)$
카메라 내부 파라미터 알면 다음과 같이 픽셀 좌표와 정규 좌표 사이 변환이 가능
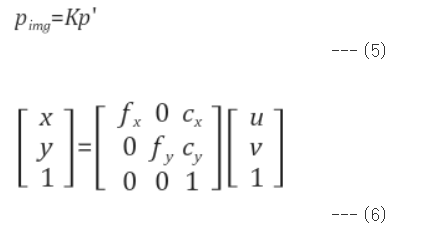
여기서 fx, fy는 초점거리, cx, cy는 주점(principal point, 광학축과 영상평면이 만나는 픽셀좌표)이며, 가운데 3 x 3 행렬을 camera matrix
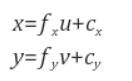
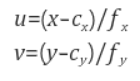
(X,Y,Z)는 월드 좌표계(world coordinate system) 상의 3D 점의 좌표, [R|t]는 월드 좌표계를 카메라 좌표계로 변환시키기 위한 회전/이동변환 행렬이며 A는 intrinsic camera matrix입니다.
출처
'개인 공부 > 컴퓨터비전' 카테고리의 다른 글
| 캘리브레이션, 카메라 파라미터 (0) | 2024.04.09 |
|---|---|
| Marching Cube (0) | 2021.08.04 |
| Affine Plane, Affine Space, Affine Transformation (0) | 2021.07.28 |
| Point Cloud (0) | 2021.07.06 |
| Sparse Convolution (0) | 2021.07.05 |




