| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 최소 #공배수 #최대 #공약수 #유클리드 #호제법 #lcm #gcd #c++ #boj #3343 #백준 #장미
- c++ #boj #
- 코딩
- c++ #입출력 #속도 #ios #sync_with_stdio #cin #cout #tie
- 22869
- hcpc
- BOJ
- graph #최단경로
- 쌤쌤쌤
- N번째큰수
- 사이클 없는 그래프
- 16202
- graph
- 투포인터 #백준 #boj #20922 #22862
- 이분탐색 #dp #11053
- 호반우 상인
- C++
- 30870
- 레드아보
- backtracking #codetree #디버깅 #삼성코테
- 백준
- 백준 #다익스트라 #dijkstra #9370 #c++
- LIS #가장긴증가하는부분수열 #
- 줄어드는수
- 진법변환 #2to10 #10to2 #이진법 #십진법 #변환 #bitset #c++
- 3343
- 20117
- 3D #Reconstruction #computer #vision #volume #metric #tsdf #kinect #fusion
- 1174
- boj #백준
- Today
- Total
hyunjin
3D Reconstruction , TSDF 본문
1. 3D Reconstruction 이란?
실제 물체의 모습이나 모양을 복원하는 과정
여러 2D images 로부터 3D image 얻는 과정
본래 image는 3D scene에서 2D plane으로 mapping, 이 과정에서 Depth(깊이) 손실
단일 이미지에선 이 선의 어느 점이 이미지에 해당하는지 결정할 수 없음.
2개의 image에서 3차원 점의 위치는 2개의 투영 광선의 교차점으로 발견 가능 => Triangulation
삼각측량법 통해 여러 2D image만을 통해 3D 물체로 복원 가능
이미지들로 부터 geometrical structure 추론하는 것
보통 카메라 위치와 internel parameter 이미지로부터 추정하는..
멀티플 이미지를 사용하므로써 3D는 정보 픽셀 와이즈 대응 문제를 해결하므로써 찾을 수 있다.
자동 대응 추정은 보통 모호하고 불안전하기 때문에 대상에 대한 사전 정보가 필요하다.
The 3D reconstruction problem is formulated as an energy minimization problem.
에너지 최소화 문제로 공식화된다.
reconstruction has a lot of applications ranging from intelligent systems like autonomous vehicles trying to understand the environment, geometry in order to navigate to biology to medical applications and many more. 매우 broad spectrum
전통적인 reconstruction pipeline

set of images → estimating the camera pose → Dense Correspondences → a set of Depth map → Depth map Fusion → 3D Reconstruction
set of images → estimating the camera pose
(feature sparse와 match 시켜 이미지에서 서로 대응하는 a few sparse features를 찾는다. 그리고 bundle 묶음이라 불리는 3D point location과 카메라 포즈를 함께 해결하는 조정문제를 해결한다.
find a few sparse features in the images correspond to each other
than you solve
what is called the bundle묶음 adjustment problem which solves for the structure the 3D point location and the camera pose together
so out comes the camera location as well as very sparse 3D reconstruction now
) -> Dense Correspondences( we want to get a dense deapth map
each of the images에 대한 and we depth this by shooting array for every pixel that project into lines onto images and then on these lines
we find correspondense so we try to fine the pixel that looks inputimage에서 대응된는 pixel)
-> a set of Depth map (for each of the input image we have a depth map 이게 full 3D reconstruction은 아님, it's just two and a half T reconstruciton ) -> Depth map Fusion (fuse depth map to a full 3D reconstruction of the scene )-> 3D Reconstruction
take two and a half depth map to project the depth information into the 3D space and then to calculate an implict surface representation by going through every voxel in the 3D space and measuring the distance to the 가까운 surface 이것을 do this for every of the input images for every the depth maps -> fuse all this information by simply averaging this implicit repersentation and then from that extracting a zero level set out again which gives you the surface and you have the final reconstruction
Volumetric Fusion
Pros :
- simple,fast,easy to implemt
- Defacto "gold standard" (KinectFusion, Voxel Hashing)
Cons
- Requires many redundant views to reduce noise
- Can't handle outliers / Complete missing surfaces
2. 3D Reconstruction 핵심 내용
핵심은 Epipolar geometry를 이용한 Triangulation 과정에 있다.
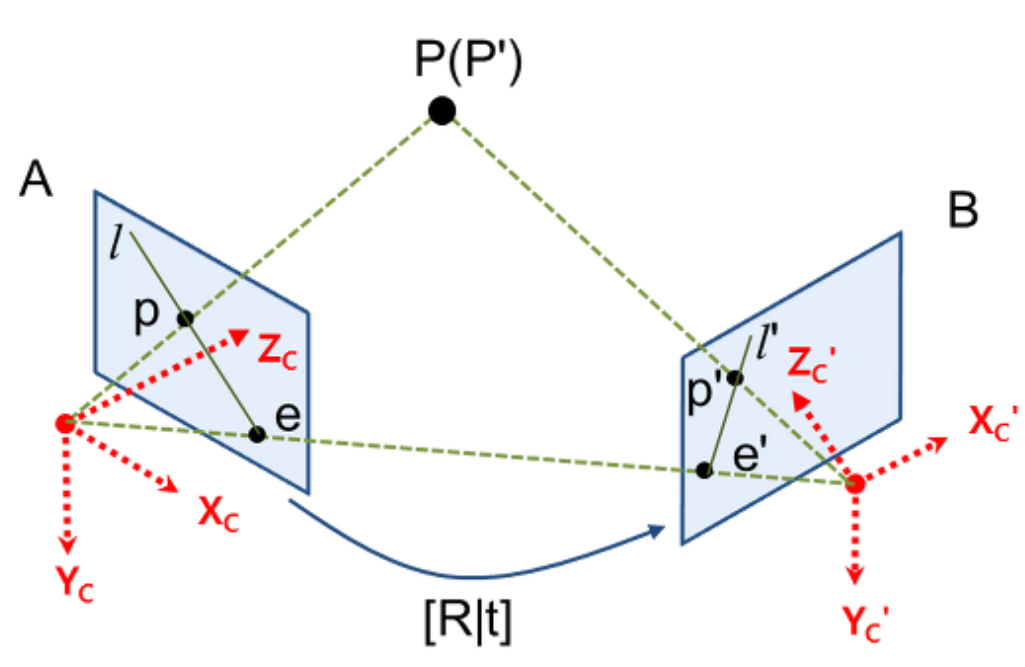
그림 1에서 스테레오 비전 즉, 2-view 비전에서 기하라고 생각하면 된다.
즉, Epipolar geometry는 동일한 사물 또는 장면에 대한 영상을 서로 다른 두 지점에서 획득했을 때,
영상 A, B의 매칭쌍 사이의 기하학적 관계를 다루는 것
두 이미지 평면 사이의 기하학적 관계가 주어지고 (카메라의 R|t) 두 이미지 평면 상의
매칭쌍 $p$ , $p'$ 이 주어지면 이로부터 원래의 3D 공간좌표 $P$ 결정할 수 있다.
핵심 내용
3D recontruction의 핵심은 epipolar geometry 이용한 triangulaion 과정에 있다.
epipolar geometry는 동일한 사물 또는 장면에 대한 영상을 서로 다른 두 지점에서 획득 했을 때 영상 A와 영상B의 매칭쌍들 사이의 기하학적 관계를 다루는 것
더 자세한 수식 이런것은 다음에... 정리
mesh : 폴리곤이 모여 하나의 3차원 물체를 만드는 것. mesh는 폴리곤이 모여 만들어진 3차원 공간상의 객체
A Truncated Signed Distance Field (TSDF)
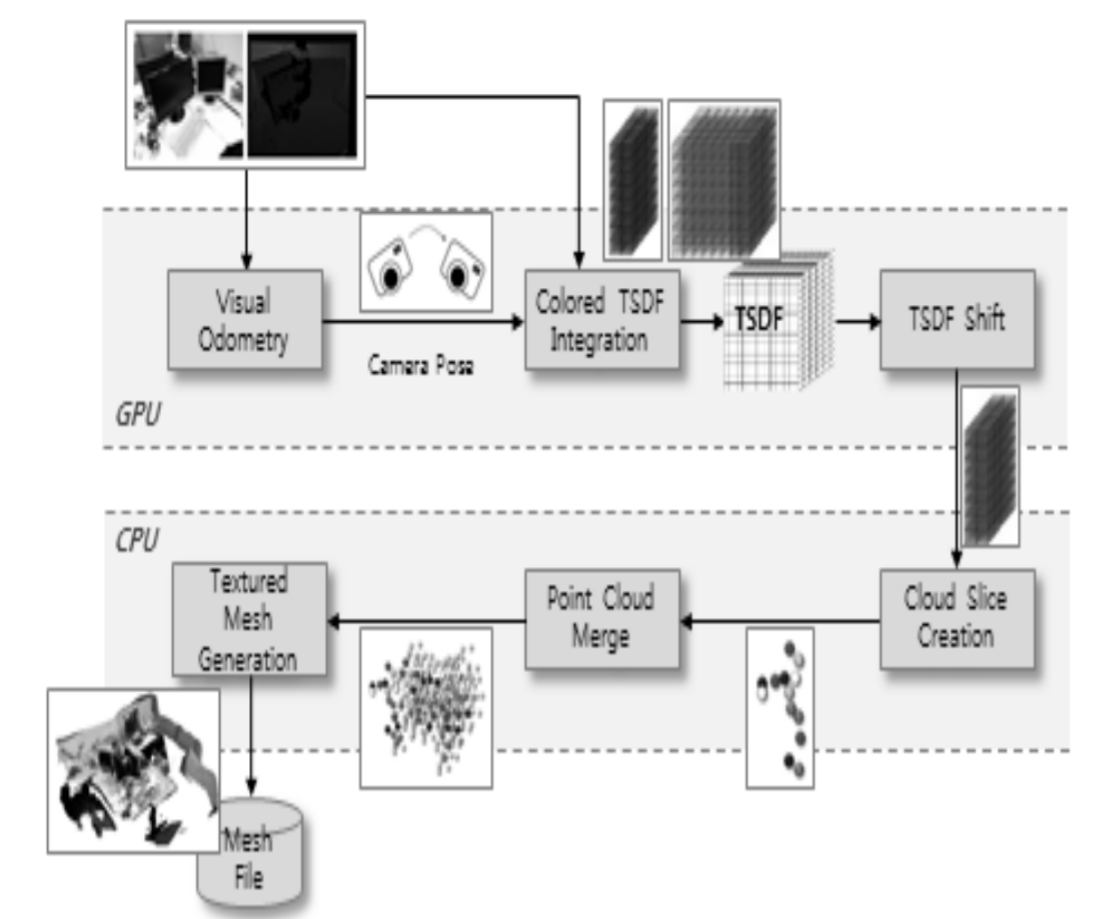
TSDF Cube Model이란,
잡음과 불확실성을 내포한 깊이 영상 으로부터 3차원 공간 표면을 효과적으로 표현하기 위해,
전체 공간을 일정한 크기의 정육면체 복셀(voxel)들로 구성된 커다란 하나의 큐브(cube)로 표현하고,
각 복셀에는 물체 표면과의 거리를 나타내는 TSDF값과 그 값의 신뢰도를 나타 내는 가중치(weight)를 함께 저장하는 방식
본 시 스템에서는 3m*3m*3m 크기의 공간을 표현할 수 있는 하나 의 TSDF 큐브를 GPU 내에 저장하며, 새로운 입력 영상이 들어올 때마다 이 영상에서 추출한 새로운 공간 정보를 TSDF 큐브로 표현한 다음, 이것을 이전 영상들로부터 구축 해놓은 TSDF 큐브에 결합함으로써 TSDF 큐브 모델을 갱 신해나간다.
만약 카메라가 3m*3m*3m 크기의 기존 공간 제한을 벗어나 새로운 영역으로 이동하게 되면, GPU 메모 리에 저장하고 있던 TSDF 큐브 모델 중 일부는 CPU가 관 리하는 RAM 기억장소로 이동하여(TSDF Shift), 점군(point cloud) 데이터 형태로 저장된다(Cloud Slice Creation). RAM 기억장소로 옮겨온 점군 슬라이스는 광역 공간을 나 타내는 전역 점군(global point cloud) 데이터 집합에 결합된 후(Point Colud Merge), 가시성을 높이기 위해 메쉬 파일 (mesh file)로 변환된다(Textured Mesh Generation)
a 3D voxel array representing objects within a volume of space in which each voxel is labeled with the distance to the nearest surface. 3D voxel array로 표현되는 물체
Numerous observations of an object from different perspectives average out noise and errors due to specular highlights and interreflections, producing a smooth continuous surface. This is a key advantage over equivalent point-cloud-centric strategies, which require additional processing to distinguish between engineered features and erroneous artifacts in the scan data. The volume can be converted to a triangular mesh using the Marching Cubes algorithm and then handed off to application-specific processes.
KinectFusion?
해당 논문은 kinect 카메라로부터 얻는 정보(pixel당 매칭되는 depth, RGB color = RGB-D)으로부터 실제 공간의 object들과 background를 3d reconstruction하는 것이다
fuse all of the depth data streamed from a Kinect scensor into a single global implicit surface model of the observed scene int real-time
참고/출처
Tum Multi-View 3D Reconstruction
3D reconstruction from multiple images 위키피디아
[TSDF]
TSDF : 3차원 장면 복원을 위한 강건한 실시간 시각 주행 거리 측정,Robust Real-Time Visual Odometry Estimation for
TSDF Fusion used in KinectFusion
3D Scene Reconstruction Joo-Hee Kim† ⋅In-Cheol Kim††
KinectFusion:Real-time Dense Surface Mapping and Tracking
Deep models for 3D reconstruction youtube
'개인 공부 > 컴퓨터비전' 카테고리의 다른 글
| Marching Cube (0) | 2021.08.04 |
|---|---|
| 좌표계, 좌표계 변환 (0) | 2021.07.30 |
| Affine Plane, Affine Space, Affine Transformation (0) | 2021.07.28 |
| Point Cloud (0) | 2021.07.06 |
| Sparse Convolution (0) | 2021.07.05 |




